Tất tần tật công thức thể tích hình trụ các loại
Các bạn học sinh thân mến, trong hình học không gian các bạn được học về cách tính của nhiều loại hình. Ví dụ như: Hình nón, hình trụ, hình chóp, hình lăng trụ, trụ tròn, trụ rỗng,…Vậy cách tính thể tích hình trụ (còn được gọi là hình trụ rỗng) là gì? Hẳn các bạn đều biết, tuy nhiên làm thế nào để ghi nhớ được cách tính thể tích hình trụ, công thức tính thể tích hình trụ lâu? Hãy note lại và học thuộc nó thôi nhé. Dưới đây sẽ là tổng hợp những công thức tính thể tích hình trụ giúp bạn ghi nhớ và tập trung hơn.

Thể tích của hình trụ tròn
Như các bạn cũng đã biết, hình có 2 mặt đáy song song và bằng nhau gọi là hình trụ tròn. Những vật dụng hình trụ tròn có thể nói đến như: Ly cốc, lọ hoa, lon sữa,…Cách tính thể tích hình trụ tròn mang nhiều ứng dụng thực thế và cũng khác là đơn giản. Công thức tính thể tích hình trụ tròn như thế nào? Các bạn xem dưới đây:
– Để tính thể tích hình trụ tròn, ta áp dụng công thức sau: V = π. r2. h
Với: V là ký hiệu thể tích
r là bán kính hình tròn mặt đáy hình trụ
h là chiều cao của hình trụ
π là hằng số ( π = 3, 14)
– Đơn vị thể tích: mét khối (m3)
– Có thể nói nguyên văn bằng lời: Muốn tính thể tích của hình trụ, ta lấy chiều cao nhân với bình phương độ dài bán kính hình tròn mặt đáy hình trụ và số pi.
Ngoài ra còn có công thức và cách tính diện tích hình trụ, diện tích hình trụ là toàn bộ không gian chiếm giữ bằng cách tính tổng S xung quanh và S 2 đáy. Còn diện tích toàn phần là diện tích của mặt quanh hình trụ không có mặt đáy.
– S (xung quanh) = 2π rh
+ r: bán kính hình trụ
+ h: chiều cao nối từ đáy tới đỉnh hình trụ
– S (toàn phần) = 2πr2 + 2πrh = 2 π r (r + h)
Trong đó:
+ r: bán kính hình trụ
+ 2 πrh : diện tích xung quanh hình trụ
+ 2 π r2: diện tích của hai đáy
=> Xem Podcast là gì? Phát hành Podcast như thế nào?
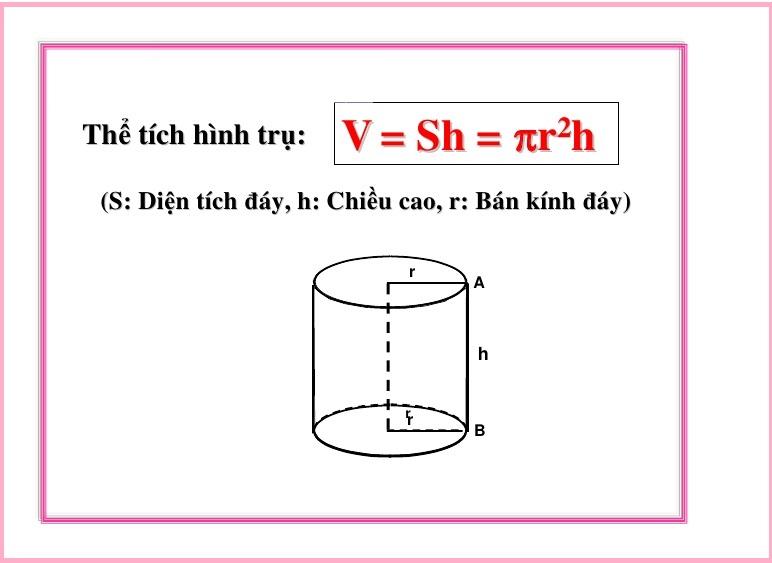
Công thức tính thể tích hình trụ
Dựa vào công thức tính thể tích hình trụ bạn có thể giải quyết những bài toán về cách tính thể tích hình trụ tròn, bán kính đáy, diện tích đáy tròn và chiều cao hình trụ.
Bài toán ví dụ:
Cho một lăng trụ tròn có bán kính mặt đáy r = 5 cm, trong khi đó, chiều cao nối từ đỉnh của hình trụ xuống đáy hình trụ có độ dài h = 9 cm . Hỏi thể tích của hình trụ này bằng bao nhiêu?
Theo đó, ta áp dụng vào công thức ta có thể tính được thể tích hình lăng trụ tròn bán kính mặt đáy hình trụ r = 4cm và chiều cao hình trụ h = 8cm. Suy ra, ta có công thức tính thể tích hình trụ như sau:
V = π x r2 x h = π x 42 x 8 = ~ 402 cm3
=> Tìm hiểu Podcast tiếng việt hay nhất
Thể tích hình lăng trụ đứng
Đối với hình lăng trụ đứng (có lăng trụ tam giác, lăng trụ tứ giác) thì thể tích của hình sẽ là diện tích đáy nhân với chiều cao. Theo đó ta có công thức tính thể tích hình lăng trụ đứng như sau:
– V = S. h
S: diện tích đáy
h: chiều cao
Vậy để tính được tính thể tích hình lăng trụ bạn cần biết được cách tính của diện tích đáy của hình lăng trụ. Công thức tính diện tích xung quanh của hình lăng trụ đứng là:
S = 1/4na2cotπ/n
n: số cạnh
a: các cạnh
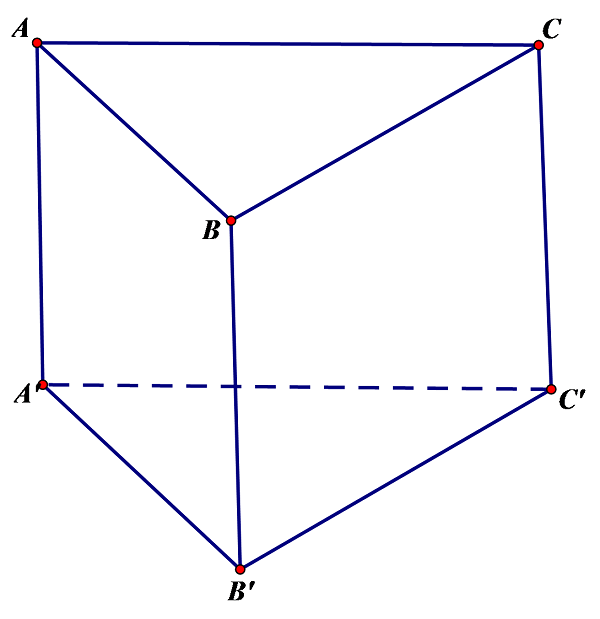
Hình lăng trụ đứng
Một ví dụ về thể tích lăng trụ tam giác để bạn hiểu thêm về cách áp dụng công thức trên.
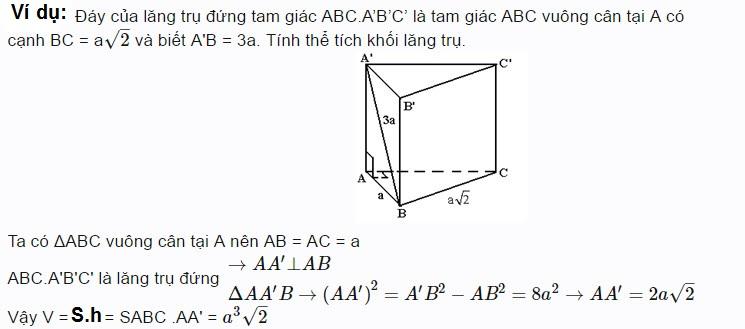
Cách tính thể tích hình lăng trụ tam giác
Với công thức thể tích hình trụ, thể tích hình lăng trụ bạn đã có thể hiểu hon về công thức tính thể tích hình trị hay thể tích hình trụ tròn, lăng trụ đứng,…Đặc biệt là với công thức thức này luôn có trong các bài tập liên quan đến hình học không gian. Có công thức tính thể tích hình trụ thì bạn sẽ dễ dàng giải quyết bài toán đưa ra. Đồng thời cũng dễ dàng thấy được các bài tập kết hợp với cách tính thể tính hình lập phương hay thể tích hình hộp chữ nhật.
=> Nghe ca khúc Ngã rẽ đời tôi
=> Cô gái vàng trong làng nhạc Cover Âu Mỹ
=> Trà Atiso và những điều bạn nên biết khi dùng
Mặt khác, các bạn cũng sẽ được làm quen khi học về hình bình hành, bởi ns cũng sẽ là các công thức tính diện tích, chu vi hình bình hành…. Để học tốt và có thể ghi nhớ lâu hơn các công thức hình học, công thức thể tích hình trụ bạn cần tham khảo, thường xuyên làm các bài tập mẫu đa dạng về cách giải.
Với việc học thuộc công thức tính thể tích hình trụ, bạn có thể yên tâm trong những bài thi. Đặc biệt là có thể tính được nhiều bài toán kể cả trong sách vở hay ngoài thực tế từ đơn giản đến phức tạp. Đồng thời cũng dễ dàng khi mà phải kết hợp với công thức tính diện tích, thể tích hình trụ và hình lập phương, hình chữ nhật.
Những chia sẻ trên về thể tích hình trụ phần nào hữu ích dành cho bạn để áp dụng vào những bài kiểm tra, bài thi có môn hình học. Chúc bạn học thật tốt và hoàn thành tốt các bài thi sắp tới nhé.
=> Tìm hiểu Podcast tiếng anh hay nhất
