Tập hợp bảng đạo hàm đầy đủ và dễ hiểu nhất
Nếu bạn đang lo lắng vì không thể nhớ nổi những công thức đã được học về đạo hàm để chuẩn bị cho các kỳ thi sắp tới tốt hơn. Hãy tham khảo bài viết dưới đây, sẽ là những tập hợp về bảng đạo hàm đầy đủ, chi tiết và dễ hiểu. Từ đó giúp bạn dễ dàng ôn luyện lại kiến thức về bảng công thức đạo hàm, bảng đạo hàm nguyên hàm, bảng đạo hàm lượng giác…cơ bản và nâng cao.

Bảng đạo hàm đầy đủ và dễ hiểu nhất
Trước khi bước vào những công thức của bảng đạo hàm bạn cần phải biết Đạo hàm là gì? Chắc chắn các bạn ai cũng phải nằm lòng về định nghĩa của đạo hàm, nhắc lại một chút nhé.
Tỷ số giữa số gia của hàm số và số gia của đối số tại điểm x0 được gọi là đạo hàm. Giá trị của đạo hàm được thể hiện chiều biến thiên của hàm số và độ lớn của biến thiên này. Đạo hàm có ý nghĩa vật lý và hình học.
Dưới đây là bảng đạo hàm đầy đủ gồm có: bảng đạo hàm cao cấp, bảng đạo hàm mở rộng các bạn cùng tham khảo:
=> Tìm Hiểu Thống Kê Podcast Tại Việt Nam

Bảng công thức đạo hàm đầy đủ
Cách tính đạo hàm bằng định nghĩa theo những quy tắc sau:
– Bước 1: Với Δx là số gia của đối số tại xo, tính:
Δy = f(xo + Δx) – f(xo)
– Bước 2: Lập tỉ số Chuyên đề Toán lớp 11. Phần này thuộc chuyên đề: Lý thuyết – Bài tập Toán 11 có đáp án
– Bước 3: Tính Chuyên đề Toán lớp 11. Phần này thuộc Chuyên đề: Lý thuyết – Bài tập Toán 11 có đáp án
=> Chú ý: Trong định nghĩa trên đây, thay xo bởi x ta sẽ có định nghĩa và quy tắc tính đạo hàm của hàm số y = f(x) tại điểm x ∈ (a, b)
Ngoài cách tính đạo hàm theo đinh nghĩa thì còn tính đạo hàm bằng máy tính. Một ví dụ về cách tính đạo hàm bẳng máy tính casino để các bạn có thể dễ hiểu hơn.
=> Tìm Hiểu Podcaster Là Gì? Danh Sách Những Podcaster Nổi Bật Nhất Hiện Nay

Cách tính đạo hàm của một đa thức
Các bạn có thể tìm hiểu thêm về tính đạo hàm bằng máy tính từ những bài tập mà thầy cô đã làm trên các trang về học tập và giải toán.
=> Xem Top 3 Cách Nghe Podcast Hiệu Quả Nhất
Ý nghĩa của đạo hàm
– Ý nghĩa hình học
Đạo hàm của hàm số f(x) tại điểm x0x0 là hệ số góc của tiếp tuyến tại điểm M(x0,f(x0))M(x0,f(x0)) đó.
=> Phương trình của tiếp tuyến tại điểm M: y−y0=f′(x0)(x−x0)y−y0=f′(x0)(x−x0)
– Ý nghĩa vật lý
Xét chuyển động thẳng s=f(t)s=f(t)
Khi đó vận tốc tức thời tại thời điểm t0t0 là: v(t0)=s′(t0)=f′(t0)v(t0)=s′(t0)=f′(t0)
Còn gia tốc tức thời tại thời điểm t0t0 là đạo hàm cấp 2 của phương trình chuyển động:
a(t0)=f′′(t0)a(t0)=f″(t0)
Giả sử điện lượng Q truyền trong dây dẫn xác định bởi phương trình:
Q=f(t)Q=f(t)
Cường độ tức thời của dòng điện tại thời điểm t0t0: I(t0)=Q′(t0)=f′(t0)
Đạo hàm có những quy tắc gì?
Bảng đạo hàm có 2 quy tắc:
+ Quy tắc cơ bản của tính đạo hàm
+ Quy tắc đạo hàm của hàm hợp số

Nguyên tắc của bảng đạo hàm
Bảng đạo hàm cơ bản có những gì?
Dưới đây là bảng đạo hàm cơ bản với những công thức mà bạn cần phải ghi nhớ, học thuộc để có thể áp dụng và làm bài tập tốt nhất. Bảng đạo hàm cơ bản gồm có:
– Đạo hàm của f(x) với x là biến số
– Đạo hàm của f(u) với u là một hàm số
– Đạo hàm của một số phân thức hữu tỉ thường gặp
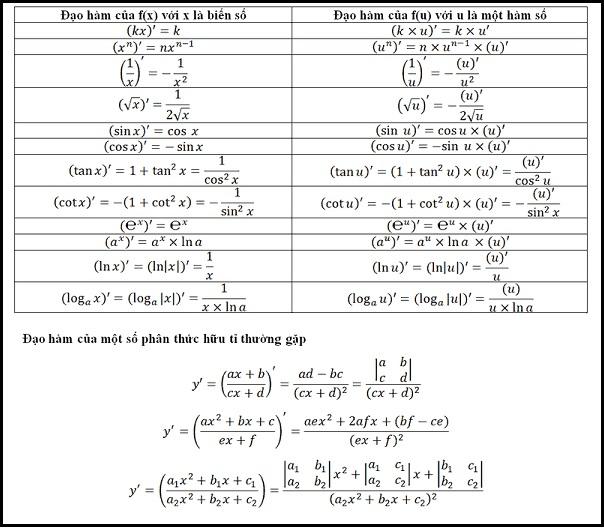
Đạo hàm của một số phân thức hữu tỉ
Bảng đạo hàm của hàm lượng giác và lượng giác ngược

Bảng đạo hàm của hàm lượng giác và lượng giác ngược
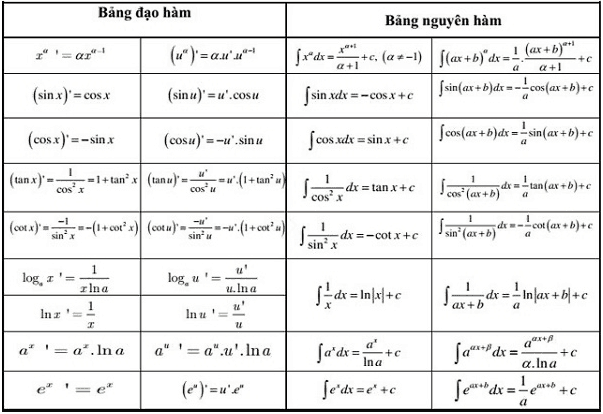
Bảng nguyên hàm và đạo hàm
Các phương pháp xác định nguyên hàm
Để xác định nguyên hàm, bạn cần tham khảo những phương pháp dưới đây để khi áp dụng vào bài tập sẽ hiệu quả nhất.
– Xác định nguyên hàm bằng định nghĩa
– Xác định nguyên hàm bằng việc sử dụng bảng các nguyên hàm cơ bản
– Xác định nguyên hàm bằng phương pháp phân tích
– Xác định nguyên hàm bằng phương pháp đổi biến số
– Xác định nguyên hàm bằng phương pháp tích phân từng phần
– Xác định nguyên hàm bằng phương pháp dùng nguyên hàm phụ
– Nguyên hàm các hàm số hữu tỉ
– Nguyên hàm các hàm số lượng giác
– Nguyên hàm các hàm số vô tỉ
– Nguyên hàm các hàm số siêu việt
Bảng công thức đạo hàm cơ bản, bảng đạo hàm cao cấp, tất cả sẽ là hành trang luôn theo bước của bạn trong chương trình toán cấp 3 cho đến những ngày tốt nghiệp.
=> Nhạc giúp bạn tập trung tinh thần học tập ở đây
Những kỳ thi tốt nghiệp, đại học bảng đạo hàm luôn đồng hành với các bạn trong chương tình toán cao cấp mà các bạn sẽ được học khi vào đại học. Chính vì vậy, việc ghi nhớ những công thức đạo hàm cơ bản và sơ cấp này là nên tảng để bạn có thể học nâng cao khi bước vào trường đại học.
Ngoài việc học thuộc công thức, định nghĩa thì bạn cần tập trung làm thật nhiều bài tập để va chạm với nhiều trường hợp. Khi đó việc giải quyết một bài toán liên quan đến đạo hàm sẽ trở nên dễ dàng hơn bao giờ hết. Đặc biệt nó sẽ giúp bạn nhớ lâi và phản ứng kịp thời khi gặp đề thi khó.
Trên đây là những chia sẻ đầy đủ về bảng đạo hàm: cơ bản, bảng đạo hàm cao cấo, bảng đạo hàm và nguyên hàm,…cùng những công thức đầy đủ nhất dành cho các bạn. Mong rằng sẽ hữu ích dành cho bạn. Chúc các bạn thành công và cố gắng học thuộc nhé.
=> Nghe đọc truyện Solo Leveling / Tôi thăng cấp một mình – MC Hương Giang full miễn phí tại đây
